The Joy Of Duplexes

In which integration brings simplification.

03 Apr 2022

This article is about cryptography, which is most commonly used in high-risk scenarios. It’s an extremely subtle and complex subject and it’s one in which I’m absolutely not an expert. The constructions, schemes, and protocols I discuss are not standardized, nor have they been analyzed by a professional or anyone else who is assuming risk for whatever you might use them for. The vibe of this post is “hey wow, look at these neat ideas” and not “everyone should use duplexes”. Govern yourself accordingly.

I’ve been playing around with a little side project lately which makes heavy use of a relatively new type of cryptographic primitive–the duplex–and I figured I should take the time to share what I’ve learned and some of the pretty profound impacts the duplex can have on designing cryptographic protocols.

In this post, we’ll talk about permutations, sponge functions, and duplexes–what they are, how they’re built, what makes them secure, and how they’re used. We’ll use a sponge function to build our own hash function, calculate message authentication codes, generate pseudo-random data, and make a stream cipher. We’ll use a duplex to do authenticated encryption, make cryptographic transcripts, create digital signatures, and build an authenticated public key encryption scheme (a.k.a. signcryption). We’ll even design our own authenticated session encryption protocol with only a duplex and an elliptic curve.

In order to do all of this, though, we need to understand what a duplex is, which means we first need to understand what a permutation is and how they’re used to build a sponge. It’s a long post, so pack a lunch. Let’s go.

Permutations

A permutation, as the name implies, shuffles things around: it’s a function which maps inputs to outputs so that no two inputs produce the same output. We pass it a fixed-size array of bits $x$; it returns another fixed-sized array $y$. We only get $y$ if we pass it $x$ again.

A good permutation from a cryptographic perspective is one which hides patterns in the input. In technical terms, it should be hard to distinguish a permutation from a random oracle. (A random oracle is a theoretical service which maps inputs to random outputs via an infinite secret lookup table; it’s impossible by definition to detect any pattern between inputs and outputs.) Ideally, the only way to tell the difference between a permutation and a random oracle is by knowing exactly what the permutation is and running the algorithm in reverse.

In that way, a block cipher with a fixed key is a kind of permutation: each unique plaintext block is mapped to a unique ciphertext block. (If it didn’t, you’d have some ciphertexts which decrypt to the wrong plaintext!) A hash algorithm, on the other hand, is not a permutation: some inputs produce the same outputs via collision. (This gets kind of important later, so keep it in mind.)

Finally, a good permutation should be constant-time: the operations it performs shouldn’t be dependent on the value of the input block. This means that an adversary can’t use timing attacks to learn about any of the data we’re passing to our permutation function.

Examples of permutation algorithms include Keccak-p (used in SHA-3), Xoodoo (used in Xoodyak), and Gimli (used in libhydrogen).

For now, imagine we have a permutation function $f: \{0,1\}^b \rightarrow \{0,1\}^b$ which maps blocks of $b$ bits to other blocks of $b$ bits in a way which makes it hard to tell what the input was.

Let’s use it to make a sponge.

Sponges

The sponge, in cryptography, is a function which absorbs an input string of arbitrary length and then squeezes an output string of arbitrary length. (Like a sponge. Get it?) It was originally defined by Guido Bertoni, Joan Daemen (co-inventor of AES), Michaël Peeters, and Gilles Van Assche as part of their design process of Keccak for the NIST SHA-3 competition. (Their design won the competition, making SHA-3 the most widely deployed sponge scheme to date.)

Sponge As Function

From the outside, a sponge is a function which takes an arbitrarily-long input value $M$ and a non-negative integer $\ell$ and returns a $\ell$-bit value:

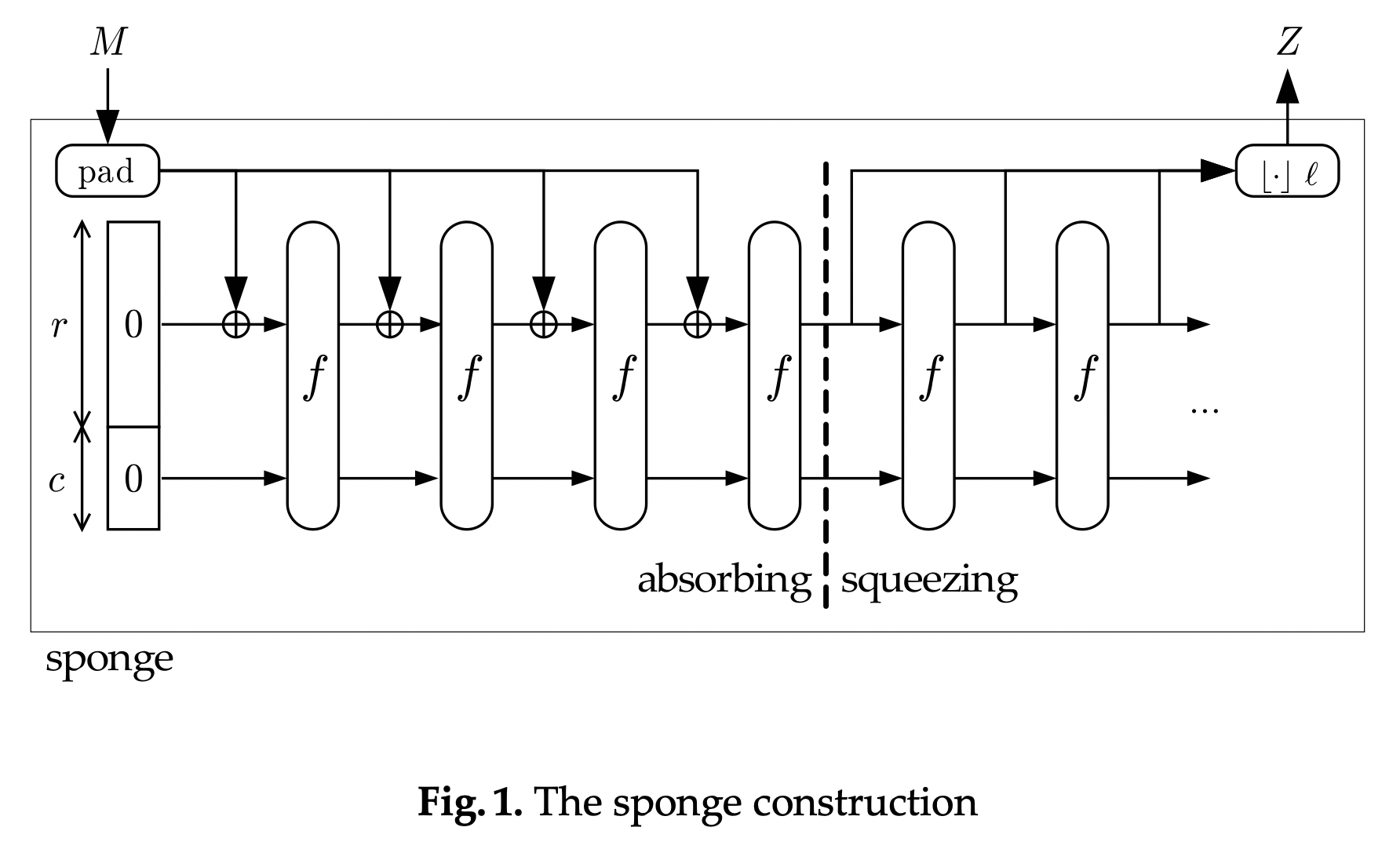
\[\begin{gather*} \text{Sponge}(M, \ell): \{0,1\}^{\mathbb{Z}^*} \times \mathbb{Z}^* \rightarrow \{0,1\}^\ell \end{gather*}\]

The implementation of a sponge starts with our permutation function $f$ and adds a state variable $S: \{0,1\}^b$ which is split into two sections: an outer section of $r$ bits and an inner section of $c=b-r$ bits. We call $b$ the sponge’s width, $r$ the sponge’s rate, and $c$ the sponge’s capacity.

Finally, we add a padding function, $P$, which maps a string $M$ of arbitrary length to a sequence of $r$-bit blocks. (The usual choice appends a $1$-bit, then $(|M| \bmod r)-2$ $0$-bits, then a final $1$-bit. Nothing fancy.)

Next, we’ll use these to build the two phases of a sponge function: $\text{Absorb}$ and $\text{Squeeze}$.

Absorbing Data

We start with the sponge’s state $S$ initialized to some zero value; it doesn’t really matter what as long as it’s a constant:

\[\begin{gather*} S \gets \{0\}^b \end{gather*}\]

We take the input string $M$ and turn it into a sequence of $r$-sized blocks with the padding function $P$. For each block $M_i$, we update the outer section of $S$ by XORing the two, then we run the entirety of $S$ through the permutation:

\[\begin{gather*} M_{0..n} \gets P(M) \\ S_{0..r} \gets S_{0..r} \oplus M_0 \\ S \gets f(S) \\ \dots \\ S_{0..r} \gets S_{0..r} \oplus M_n \\ S \gets f(S) \\ \end{gather*}\]

Notice that we’re only writing to $S_{0..r}$, the outer section of $S$, but we pass the whole of $S$ to our permutation function, making the final value of $S$ dependent on both sections.

Squeezing Data

Once we’re done absorbing data, we can squeeze an $\ell$-bit value $Z$ out of the state.

If $\ell≤r$, we return the first $\ell$ bits of the outer section of $S$:

\[\begin{gather*} Z \gets S_{0..\ell} \\ S \gets f(S) \end{gather*}\]

If $\ell>r$, we iterate the process, returning bytes from $S_{0..r}$ and updating $S$ with our permutation:

\[\begin{gather*} Z_{0..r} \gets S_{0..r} \\ S \gets f(S) \\ Z_{r..\ell} \gets S_{0..\min{(r, \ell)}} \\ S \gets f(S) \end{gather*}\]

Again, notice that we’re only reading from outer section of $S$, but each successive value of $S$ depends on both the outer and inner sections of the previous value.

The resulting construction looks like this (from Duplexing the sponge by Bertoni et al.):

A visualization of the sponge construction

Picking Parameters

When absorbing or squeezing, we only directly write to and read from the outer section of the sponge’s state, $S_{0..r}$. The inner section, $S_{r..b}$, is only used as input for our permutation function $f$, and the only thing we write to it is the output of $f$. The inner section of $S$ acts a reservoir of bits that an adversary either has to hold constant or never gets to see, depending on what we’re doing. This means that the ratio of the sponge’s rate $r$ to its capacity $c$ is critical.

If our sponge’s capacity is too small relative to its rate, it becomes feasible for an adversary to use the output of a sponge function to recreate the sponge’s entire state. For example, a sponge with $c=1$ would mean an adversary with an $r$-bit block of output would only need to try $2$ possible values in order to recover the full contents of $S$, at which point they could re-create the sponge’s previous states and produce arbitrary outputs.

If our sponge’s rate is too small relative to its capacity, its performance suffers due to the overhead of the permutation function. For example, a sponge with $r=1$ would have to run the permutation function for each bit of input and output.

The designers of sponge functions pick their $r$ and $c$ values carefully to balance speed and security. This will become clearer as we start building cryptographic operations with our sponge.

Message Digests

The natural use for a sponge function is as a cryptographic hash function. We pick a digest length, $n$, and pass our message $m$ to get back an $n$-bit digest:

\[\begin{gather*} d \gets \text{Sponge}(m, n) \end{gather*}\]

This is essentially how SHA-3 works.

Two things make this secure: first, the strength of our permutation function $f$; second, the fact that the inner section of $S$ acts as a reservoir of unmodifiable bits.

Consider an adversary trying to find a message $m$ which produces a fixed digest $d$ (i.e. trying to break its pre-image resistance) with a sponge function whose parameters are $b=384$, $r=256$, $c=128$. To keep it simple, we’ll imagine they’re trying to find a short $m$ such that $|m|≤r$ (i.e. the absorb phase consists of a single iteration of $f$, and $S$ is all zeroes to begin with).

Our adversary is therefore trying to find some state value $S'=P(m')||\{0\}^c$ such that $f(S')$ begins with the digest $d$. If our permutation is strong–if it’s hard to distinguish between our permutation and a random oracle–our adversary is stuck having to try all of the $2^{128}$ possible values of the inner section of $S$.

Note that because the input to a sponge function is always padded, it’s not vulnerable to length-extension attacks, unlike Merkle–Damgård constructions (e.g. MD5, SHA1, SHA-256): given $H(m)$, it’s not possible to easily calculate $H(m||x)$. That’s because $H(m)$ is actually $H(P(m))$, and our padding function $P$ is non-commutative, so $P(m||x) \not= P(m)||P(x)$.

Message Authentication Codes

The fact that sponges aren’t vulnerable to length-extension attacks means we can securely extend our message digest construction to calculate message authentication codes (MACs). We concatenate the secret key $k$ and message $m$ into a single input and squeeze an $n$-bit authentication tag $t$:

\[\begin{gather*} t \gets \text{Sponge}(k||m, n) \end{gather*}\]

This is essentially how cSHAKE and KMAC work.

It superficially resembles the kind of naive MAC construction that gets people in trouble, e.g. $\text{MD5}(k||m)$, but remember that the sponge, unlike most hash functions, isn’t vulnerable to length-extension attacks. As long as $k$ is constant size, it’s secure.

(You can run into trouble if $k$ is variable size. Proper standards like KMAC pad the key to a constant size as well as add the output length and other domain separation data to the input. If you’re trying to create a MAC of multiple pieces of information, you have to develop a padding scheme like TupleHash to ensure those different pieces of information don’t overlap in the input space or use an existing scheme. More about that in a bit.)

Let’s look at what makes our sponge-based MAC function secure. For simplicity’s sake, let’s assume $|k||m|$ and $t$ are both less than $r$ (i.e. both absorb and squeeze phases involve a single iteration of $f$). Our MAC algorithm looks like this:

\[\begin{gather*} m_0 \gets P(k||m) \\ S_{0..r} \gets S_{0..r} \oplus m_0 \\ S \gets f(S) \\ t \gets S_{0..n} \end{gather*}\]

Consider an adversary who is trying to forge a tag $t'$ for a message $m'$ without knowing the key $k$. Even if they can see an arbitrary number of messages and tags created with $k$, they’re still stuck trying to recreate the inner section of $S$ after the absorb phase. If that’s big enough, then trying to forge a tag is infeasible.

Extendable-Output Functions (XOFs)

So far we’ve only been using short outputs of the sponge, but it’s entirely possible to produce longer outputs. Let’s say we need a lot of pseudo-random data we can derive from a high-entropy value $x$. We can pass $x$ to our sponge function and squeeze as many bits as we need:

\[\begin{gather*} z \gets \text{Sponge}(x, n) \end{gather*}\]

Remember that the squeeze phase, when used to produce multiple blocks of output, looks like this:

\[\begin{gather*} S \gets f(S) \\ z_0 \gets S_{0..r} \\ S \gets f(S) \\ z_1 \gets S_{0..r} \\ S \gets f(S) \\ z_2 \gets S_{0..r} \\ \dots \end{gather*}\]

Each additional block of output can be calculated in an incremental fashion, meaning that it’s easy to build an abstraction on top of this which produces an indefinite series of bits for a given input: an extendable-output function (XOF). How secure is it?

Consider an adversary who doesn’t know the seed value $x$ but can see a single block of output $z_i$. What would they need to do to predict the next block $z_{i+1}$? If the sponge’s capacity was zero, then it would be simple: $z_{i+1}=f(z_i)$. Likewise, an adversary trying to determine the previous block could calculate $z_{i-1}=f^{-1}(z_i)$ if the sponge’s capacity didn’t exist. But a sponge with a large enough capacity makes it infeasible for an adversary to predict output without the seed value $x$.

Now, remember that $f$ is a permutation and not a compression function–it’s shuffling bits around in $S$ without collision. This is where that matters. A compression function has some probability that $f(S) = f(S')$. As that function is iterated, that probability increases, and the number of possible values for $S$ decreases, reducing the security. Thankfully, we’re using a permutation for $f$, which means we’re not creating those internal collisions as we produce output. Thus, the security of our sponge stays constant relative to the strength of $f$, allowing us to produce a long stream of effectively pseudo-random bits.

Stream Ciphers

Since we’ve got an unbounded stream of pseudo-random bits, let’s go ahead and make a stream cipher. We pass our sponge function a concatenated key $k$ and nonce $n$ and XOR our plaintext $p$ with the output:

\[\begin{gather*} c \gets p \oplus \text{Sponge}(k||n, |p|) \end{gather*}\]

Decrypting is the same thing, only with the ciphertext $c$ as input:

\[\begin{gather*} p \gets c \oplus \text{Sponge}(k||n, |c|) \end{gather*}\]

As with the XOF, this is secure if our permutation is strong and the sponge’s capacity is big enough. An adversary who knows $n$ but not $k$ will be left trying to reconstruct the inner section of $S$, unable to reconstruct the output, and therefore unable to decrypt $c$. And because we can incrementally produce the keystream, we can encrypt streams of data without buffering.

Of course, stream ciphers by themselves are not very secure. If we accidentally re-use a nonce, an adversary can calculate $p_0 \oplus p_1$, which violates the confidentiality of the plaintexts. Also, an adversary can flip bits in the ciphertext to produce alternative plaintexts that we might not be able to detect (e.g. pay me $100 could turn into give Mal $5). We could solve this problem with the sponge function, but it starts to get gnarly: once we’re done encrypting the plaintext we’d need to pass the ciphertext to another sponge function to create a MAC, but then we’re talking about a two-pass algorithm.

To elegantly solve this problem–and many, many others–we’ll need to graduate from the sponge and build a duplex.

Duplexes

A duplex, like a sponge, has a permutation function $f$, a rate $r$, a capacity $c$, a state variable $S$ divided into an $r$-bit outer section and a $c$-bit inner section, and a padding function $P$. The big difference is that a duplex is a stateful object, not a function–instead of a single absorb phase and a single squeeze phase, it maintains its state across an arbitrary sequence of absorb and squeeze phases.

The duplex was invented by Bertoni, Daemen, Peeters, and Van Assche (again) as part of their continued work on permutation-based cryptography. Examples of duplexes include Mike Hamburg’s STROBE and Daemen et al.’s Xoodyak, a finalist in NIST’s Lightweight Cryptography competition. (Xoodyak’s my personal favorite.)

Duplex As Object

It’s helpful to consider the duplex as an object with an API:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(\sigma) \\ \text{Squeeze}(\ell): \mathbb{Z}^* \rightarrow \{0,1\}^\ell \end{gather*}\]

$\text{Init}$ creates a new duplex, initializing $S$ with a zero value:

\[\begin{gather*} S \gets \{0\}^b \end{gather*}\]

$\text{Absorb}(\sigma)$ updates the duplex’s state with an arbitrary string $\sigma$ in exactly the same way as the absorb phase of our sponge function.

$\text{Squeeze}(\ell)$ returns an $\ell$-byte string and updates the duplex’s state, iterating and truncating as necessary just like the squeeze phase of our sponge function.

Our $\text{Sponge}(M, \ell)$ function, when mapped to a duplex, becomes this:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(M) \\ \text{Squeeze}(\ell) \end{gather*}\]

The duplex construction itself looks like this (from Duplexing the sponge by Bertoni et al.):

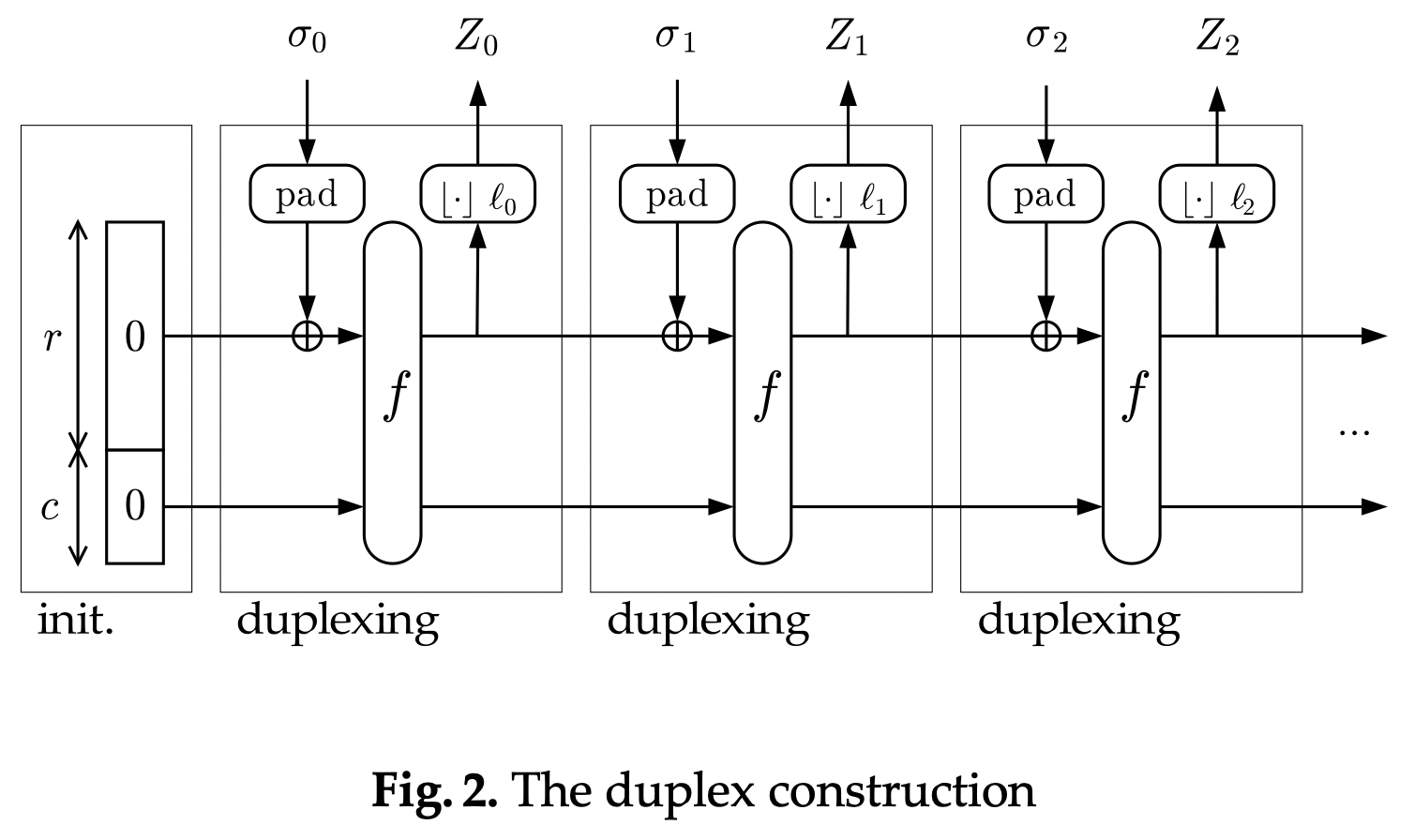
A visualization of the duplex construction

There are two major differences between a sponge function and a duplex.

First, a duplex’s inputs and outputs are non-commutative. That is, $\text{Absorb}(a)$ and $\text{Absorb}(b)$ is not the same as $\text{Absorb}(a||b)$, and $\text{Squeeze}(a)$ and $\text{Squeeze}(b)$ is not the same as $\text{Squeeze}(a+b)$. With a duplex, those produce entirely different states and thus entirely different outputs.

Second, where the sponge is limited to a single absorb phase and a single squeeze phase, the duplex can alternate between series of $\text{Absorb}$ operations and $\text{Squeeze}$ operations indefinitely.

These two changes enable us to build a frankly staggering array of cryptographic operations.

Authenticated Encryption

Let’s start with our original motivation for the duplex: authenticated encryption. The sponge gave us an XOF and thus a stream cipher, but in order to authenticate ciphertexts we’d need to use another sponge function to create a MAC or something. We can do better with the duplex.

We initialize a duplex, absorb a key $k$ and nonce $n$ and XOR our plaintext $p$ with the output much like we did with the sponge, but after that we absorb $p$ and squeeze an $m$-bit authentication tag $t$:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(k) \\ \text{Absorb}(n) \\ c \gets p \oplus \text{Squeeze}(|p|) \\ \text{Absorb}(p) \\ t \gets \text{Squeeze}(m) \end{gather*}\]

Superficially, this looks a little like the dreaded MAC-then-Encrypt construction because we’re absorbing $p$, then squeezing a tag $t$. The critical difference, however, is that $t$ isn’t only derived from $p$–it’s derived from the same state which produced the keystream to make $c$. By absorbing $p$, we ensure that $t$ seals both the plaintext $p$ and the ciphertext $c$.

We can see how this plays out when we decrypt $c$:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(k) \\ \text{Absorb}(n) \\ p' \gets c \oplus \text{Squeeze}(|c|) \\ \text{Absorb}(p') \\ t' \gets \text{Squeeze}(m) \\ t \stackrel{?}{=} t' \end{gather*}\]

If an adversary modifies $c$, then $p' \not= p$ and therefore $t' \not= t$.

This can be extended to a full AEAD by adding $\text{Absorb}(d)$ after absorbing the nonce. In fact, if we’ve got more than one piece of data to authenticate, we can add more $\text{Absorb}$ calls. There’s no need to devise our own padding scheme here. (You’ll still need to use a constant-time comparison for the authentication tag, though.)

It’s worth noting here that here, unlike with the sponge function, we’re starting to build cryptographic constructions which integrate the properties of multiple other constructions. Here we begin with what looks like a stream cipher but then turns into something more like a MAC, producing both ciphertext and tag with the same underlying primitive. In contrast, the GCM mode (e.g. AES-128-GCM) combines a block cipher (e.g. AES), a counter mode of operation, GMAC, a polynomial MAC algorithm, and a number of very specific padding functions to produce the same results.

Cryptographic Transcripts

The fact that the $\text{Absorb}$ operations aren’t commutative opens up some interesting possibilities. For example, we can create a transcript of higher-level operations and have cryptographic assurances that the transcript has not been altered or that another party performing the same actions hasn’t diverged from the same sequence. That’s a pretty abstract concept, so let’s use the example of ensuring that two users are actually the same. We initialize a duplex, absorb the pieces of data which identify the user, and finally squeeze a cryptographic identifier:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(\texttt{user.email}) \\ \text{Absorb}(\texttt{user.name}) \\ \text{Absorb}(\texttt{user.phone\_number}) \\ I \gets \text{Squeeze}(n) \\ \end{gather*}\]

This is similar to using a hash function $H(E||N||P)$, but because the duplex pads its inputs, it preserves each pieces of data as independent inputs. We can even add semantic information to ensure domain separation:

\[\begin{gather*} \text{Absorb}(\texttt{"phone\_number"+user.phone\_number}) \end{gather*}\]

This might be a little heavy-handed for user identifiers, but the ability to create a transcript of operations with cryptographic assurance of their semantic integrity turns out to be incredibly useful.

Digital Signatures

By combining our duplex with a well-defined elliptic curve like ristretto255, we can turn a cryptographic transcript into a sophisticated digital signature. For example, let’s create an EdDSA-style Schnorr signature of a message $m$ given the signer’s key pair $(d, Q)$.

Moon Math Primer

But first, we need to talk about elliptic curves.

Elliptic curves are awesome but don’t make a lot of intuitive sense to folks who are familiar with other cryptographic things like hash functions and encryption algorithms, so here’s a quick primer on what’s in play.

A scalar is a like a regular integer in that you can do arbitrary arithmetic with them. Scalars are usually notated using lowercase variables like $d$ and $k$. You can turn an arbitrary string of bits $\{0,1\}^n$ into a scalar by reducing them to fit into the space of possible scalar values:

\[\{0,1\}^n \bmod \ell \in \{0 \dots \ell\}\]

A point is a set of coordinates to a point on the elliptic curve and notated using uppercase variables like $Q$ and $G$. $G$ is the generator point, which is a point on the curve everyone agreed to use as a constant. You can add points together and you can subtract one point from another, but you can’t multiply or divide them.

You can multiply a point $Q$ by a scalar $d$ (notated $[d]Q$) in that you can add $Q$ to itself $d$ times. Calculating $[x]Y$ is super cheap; going from $[x]Y$ to either $x$ or $Y$ is functionally impossible.

Private keys are scalars which are picked at random from the set of all possible scalars. A public key $Q$ for a private key $d$ is calculated by adding the generator point $G$ to itself $d$ times: $Q=[d]G$. Again, it’s easy to go from private key to public key; it’s effectively impossible to go from public key to private key.

A longer, gentler introduction to the subject can be found here.

Ok, back to our digital signature scheme.

Signing A Message

First, we initialize a duplex and use it to absorb the message $m$ and the signer’s public key $Q$:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(Q) \\ \text{Absorb}(m) \end{gather*}\]

Next, we generate a random commitment scalar $k$, then calculate and absorb the commitment point $I$:

\[\begin{gather*} k \stackrel{\$}{\gets} \{0,1\}^{512} \bmod \ell \\ I \gets [k]G \\ \text{Absorb}(I) \end{gather*}\]

Finally, we squeeze a challenge scalar $r$ and calculate the proof scalar $s$:

\[\begin{gather*} r \gets \text{Squeeze}(512) \bmod \ell \\ s \gets dr+k \end{gather*}\]

The resulting signature is $I||s$.

Verifying A Signature

The signature can be verified like this:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(Q) \\ \text{Absorb}(m) \\ \text{Absorb}(I) \\ r' \gets \text{Squeeze}(512) \bmod \ell \\ I' \gets [s]G - [r']Q \\ I \stackrel{?}{=} I' \end{gather*}\]

Now, EdDSA signatures are entirely possible to create with regular hash algorithms–Ed25519 uses SHA2-512), but by using a duplex we get a number of benefits.

For one, it allows us to easily establish cryptographic dependence between values. For Schnorr signatures, we need the challenge scalar $r$ to be dependent on all the inputs: $Q$, $m$, and $I$. If we don’t include the signer’s public key $Q$, then it’s possible to find another public key which produces the same signature for the same message. If we don’t include the message $m$, then what are we even signing? Likewise, if we don’t include the commitment point $I$, then it becomes possible to produce an infinite number of alternate valid signature/public key pairs given a signed message.

For two, we’re not limited to signing a single bitstring. We can easily sign arbitrarily structured data as long as it can be traversed in a deterministic fashion. A set of financial transactions, a complex mathematical structure, a conversation between services, whatever. You can even use duplexes to securely structure zero-knowledge proofs.

For these more complex protocols, it’s helpful to think of the duplex as establishing a transcript of all the values being used. If we absorb all the inputs, the outputs will always be cryptographic dependent on them, giving adversaries far fewer opportunities to modify them.

Signcryption

Now that we’ve got encryption and digital signatures going, we can combine the two to produce a signcryption scheme, which provides both confidentiality and authenticity in the public key setting. Given a sender’s key pair $(d_S, Q_S)$, a receiver’s public key $Q_R$, and a plaintext $p$, we start by initializing a duplex and absorbing everyone’s public keys:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(Q_S) \\ \text{Absorb}(Q_R) \end{gather*}\]

Next we generate an ephemeral key pair $(d_E, Q_E)$ and absorb the public key:

\[\begin{gather*} d_E \stackrel{\$}{\gets} \{0,1\}^{512} \bmod \ell \\ Q_E \gets [d_E]G \\ \text{Absorb}(Q_E) \end{gather*}\]

After that we calculate the Elliptic Curve Diffie-Hellman (ECDH) shared secret between the ephemeral private key $d_E$ and the receiver’s public key $Q_E$, $K$, and absorb it, effectively using it as a symmetric key:

\[\begin{gather*} K \gets [d_E]Q_R \\ \text{Absorb}(K) \end{gather*}\]

Now that we’ve got a duplex keyed with a secret, we encrypt and absorb $p$:

\[\begin{gather*} c \gets p \oplus \text{Squeeze}(|p|) \\ \text{Absorb}(p) \\ \end{gather*}\]

At this point we have a duplex which is effectively a transcript of all the critical information we have: the sender’s public key, the receiver’s public key, the ephemeral public key, the ECDH shared secret, and the plaintext. If we squeezed an authentication tag here, we’d essentially have created ECIES using just two cryptographic primitives. But we can improve on that, so let’s integrate our Schnorr signature scheme:

\[\begin{gather*} k \stackrel{\$}{\gets} \{0,1\}^{512} \bmod \ell \\ I \gets [k]G \\ \text{Absorb}(I) \\ r \gets \text{Squeeze}(512) \bmod \ell \\ s \gets {d_S}r+k \end{gather*}\]

The final ciphertext is $C=Q_E||c||I||s$, which we can unsigncrypt (yes, that’s what they call it) like this:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(Q_S) \\ \text{Absorb}(Q_R) \\ \text{Absorb}(Q_E) \\ K \gets [d_R]Q_E \\ \text{Absorb}(K) \\ p' \gets c \oplus \text{Squeeze}(|c|) \\ \text{Absorb}(p') \\ \text{Absorb}(I) \\ r' \gets \text{Squeeze}(512) \bmod \ell \\ I' \gets [s]G - [r']Q_S \\ I \stackrel{?}{=} I' \end{gather*}\]

The receiver doesn’t know the ephemeral private key $d_E$, so they calculate the ECDH shared secret as $[d_R]Q_E$ because $[d_E]Q_R=[d_R]Q_E=[d_Ed_R]G$. Likewise, they don’t know the sender’s private key $d_S$, so they verify the signature using their public key $Q_S$.

The really cool thing is that our signcryption construction offers a much stronger degree of security than most because using a duplex allows us to seamlessly integrate our encryption and digital signature algorithms.

Security Through Integration

Because we’re using a duplex, our signcryption scheme is stronger than the generic schemes which combine separate public key encryption and digital signature algorithms: Encrypt-Then-Sign ($\mathcal{EtS}$) and Sign-then-Encrypt ($\mathcal{StE}$).

An adversary attacking an $\mathcal{EtS}$ scheme can strip the signature from someone else’s encrypted message and replace it with their own, potentially allowing them to trick the recipient into decrypting the message for them. That’s possible because the signature is of the ciphertext itself, which the adversary knows.

With our scheme, on the other hand, the digital signature isn’t of the ciphertext alone. A standard Schnorr signature scheme like Ed25519 derives the challenge scalar $r$ from a hash of the signer’s public key and the message being signed (i.e. the ciphertext). Our challenge scalar, on the other hand, is derived from the duplex’s state, which depends on (among other things) the ECDH shared secret $K$ and the plaintext message $p$. Unless our adversary already knows $K$ (the secret key that $p$ is encrypted with) and $p$ (the plaintext they’re trying to trick someone into giving them), they can’t create their own signature (which they’re trying to do in order to trick someone into giving them $p$). You can see how that might be hard for them.

An adversary attacking an $\mathcal{StE}$ scheme can decrypt a signed message sent to them and re-encrypt it for someone else, potentially posing as the original sender. For example, you send a sternly-worded letter to your manager, informing them that you hate your job and are quitting. Your boss decrypts the message, keeps the signed plaintext, and several months later encrypts it with your new manager’s public key and sends it to her. If the message is sufficiently generic (e.g. I hate this job and am quitting.), it looks like an authentic message from you to your new manager and you’re out of a job.

Our duplex-based scheme isn’t vulnerable to this kind of attack, thankfully, because, again, the challenge scalar $r$ is dependent on the duplex’s state, which in addition to the plaintext message $p$ also includes the ECDH shared secret $K$ and all the public keys. An adversary can duplicate the duplex’s state prior to the $\text{Absorb}(K)$ operation, but no further.

Security Through Composition

The fact that we can tightly integrate our encryption and digital signature algorithms without falling prey to the same attacks as the generic constructions means we end up with a stronger scheme than even very modern standards, like HPKE. HPKE provides an authenticated scheme in the form of the $\text{AuthEncap}$ KEM, but it’s vulnerable to very sneaky type of attack: key compromise impersonation. Key compromise impersonation (KCI) occurs when a scheme allows an adversary who compromises a user’s private key to forge messages from other users which the compromised user will believe are authentic.

For example, let’s say our adversary compromises the victim’s private key $d_V$. The adversary can take an arbitrary public key–let’s say Beyoncé’s key, $Q_B$–and use it to calculate the shared secret Beyoncé would use if she actually sent the victim a message: $[d_V]Q_B=[d_B]Q_V=[d_Bd_V]G$. If the authenticity of the message depends entirely on only the sender and receiver knowing that shared secret, as with HPKE or ECIES, the adversary could pose as Beyoncé to their victim, which would be an emotionally crushing kind of catfishing.

Our signcryption scheme, on the other hand, is immune to these particular shenanigans. The receiver of a message can verify the signature but cannot create one themselves; therefore, an adversary with the same power as the receiver (i.e. with knowledge of their private key) cannot forge a signature from someone else.

Security Through Simplicity

Finally, it’s worth stepping back and appreciating the parsimony of this approach. It’s totally possible to build signcryption constructions out of traditional primitives like block ciphers, but the degree of complexity (and the resulting risk of screwing something) is dramatically higher. For example, a design with similar properties might pass the ECDH shared secret point to HKDF-SHA2-512 and extract an AES key, CTR nonce, and HMAC-SHA2-512 key, then use Ed25519 (which also requires SHA2-512) to sign (but not transmit) the MAC of the ciphertext. Like, I think that’d work?

But you’re talking about an implementation which requires AES, SHA2-512, the twisted Edwards form of Curve25519, and probably the Montgomery form of Curve25519 (for X25519) as primitives, plus implementations of HKDF, HMAC, CTR mode, and Ed25519.

Compare that to our construction, which requires a duplex (e.g Xoodyak) and an elliptic curve (e.g. Ristretto255). (Admittedly, Ristretto255 is based on the Edwards twist of Curve25519, but NIST’s P-256 would work, too.)

Session Encryption

As a final example of what you can do with a duplex, let’s talk about session encryption. Imagine we’ve got two people that want to securely talk to each other over a (reasonably) reliable network (e.g. TCP). They want to know that their conversation is confidential (i.e. no one can eavesdrop) and authentic (i.e. no one can alter what’s said). (Obviously these two should use TLS 1.3 and be done with it, but let’s see what we can do ourselves.)

We’ve got a sender (with a static key pair $(d_S, Q_S)$) and a receiver (with a static key pair $(d_R, Q_R)$).

The sender begins by generating an ephemeral key pair $(d_S^E, Q_S^E)$ and transmitting their ephemeral public key $Q_S^E$ to the receiver. The receiver generates their own ephemeral key pair $(d_R^E, Q_R^E)$ and transmits their ephemeral public key $Q_R^E$ back the sender. They both initialize duplexes and absorb all of the public keys in the same order:

\[\begin{gather*} \text{Init}() \\ \text{Absorb}(Q_S) \\ \text{Absorb}(Q_S^E) \\ \text{Absorb}(Q_R) \\ \text{Absorb}(Q_R^E) \\ \end{gather*}\]

Next, both sender and receiver calculate two ECDH shared secrets: $K_0$, between the receiver’s ephemeral key pair and the sender’s static key pair, and $K_1$, between the sender’s ephemeral key pair and the receiver’s static key pair.

On the sender’s side:

\[\begin{gather*} K_0 \gets [d_S^E]Q_R \\ K_1 \gets [d_S]Q_R^E \\ \text{Absorb}(K_0) \\ \text{Absorb}(K_1) \end{gather*}\]

On the receiver’s side:

\[\begin{gather*} K_0 \gets [d_R]Q_S^E \\ K_1 \gets [d_R^E]Q_S \\ \text{Absorb}(K_0) \\ \text{Absorb}(K_1) \end{gather*}\]

Next, both sender and receiver clone their duplexes into incoming and outgoing duplexes (after all, a duplex is just a state variable $S$). Using their outgoing duplexes, they both create Schnorr signatures of the outgoing duplexes’ states. For example, on the sender’s side:

\[\begin{gather*} k_S \stackrel{\$}{\gets} \{0,1\}^{512} \bmod \ell \\ I_S \gets [k_S]G \\ \text{Absorb}(I_S) \\ r_S \gets \text{Squeeze}(512) \bmod \ell \\ s_S \gets d_Sr_S+k_S \end{gather*}\]

The sender transmits their signature $I_S||s_S$ to the receiver and the receiver responds with their signature $I_R||s_R$, at which point both parties use their incoming duplexes to verify the signatures. For example, on the receiver’s side:

\[\begin{gather*} \text{Absorb}(I_S) \\ r_S' \gets \text{Squeeze}(512) \bmod \ell \\ I_S' \gets [s_S]G - [r_S']Q_S \\ I_S \stackrel{?}{=} I_S' \end{gather*}\]

If the signatures are valid, the two parties have established a confidential and authentic channel of communication to each other. When the sender wants to send a message, they can use the outgoing duplex’s current state to encrypt the message and generate and authentication tag:

\[\begin{gather*} c \gets p \oplus \text{Squeeze}(|p|) \\ \text{Absorb}(p) \\ t \gets \text{Squeeze}(m) \end{gather*}\]

Likewise, when they receive a message, they can use their incoming duplex to decrypt and authenticate:

\[\begin{gather*} p' \gets c \oplus \text{Squeeze}(|c|) \\ \text{Absorb}(p') \\ t' \gets \text{Squeeze}(m) \\ t \stackrel{?}{=} t' \end{gather*}\]

Instead of a static key, this effectively creates a session encryption system with a rolling key, with the duplex’s state being cryptographically dependent on every prior operation. In order to eavesdrop, an adversary would have to reconstruct the inner section of the duplex’s state. If an adversary alters a message, the receiver’s state would diverge from the sender’s, making any communication impossible. Like our signcryption construction, the handshake provides what’s called “insider security”, in that it maintains confidentiality if the sender is compromised and authenticity if the receiver is compromised.

Again, this is a toy protocol. Our sender and receiver should use TLS. But it’s worth noting that we created a toy mutually-authenticated key exchange with streaming, authenticated encryption in what might be a couple of hundred lines of code in a way which makes it incredibly clear to document and analyze and all of that using just two cryptographic primitives.

Neat, huh?

tl;dr

The duplex is a profoundly useful cryptographic primitive which allows us to build sophisticated cryptosystems in a robust and reliable way. You can use a duplex to implement message digests, MACs, PRFs, stream ciphers, AEADs, and more using a single cryptographic primitive whose security reduces entirely to the strength of a single permutation function. Duplexes make it easier to build high-level constructions and protocols, but it’s such a new concept that relatively little work has been done in terms of standardizing specific constructions or developing security proof techniques for analyzing duplex-based protocols. Hopefully everyone who makes it to the end of this overly-long article will be as enthusiastic as I am about the future of the cryptographic duplex (and permutation-based cryptography, generally). Here’s a ten-hour video of some mountains as a reward.

Updated April 03, 2022

Clarified the definition of permutation. Thanks, quasi_qua_quasi!

Thanks to various Fiascans and Jeff Hodges for reviewing this post. Thanks to Niki Hale for suggesting putting a video at the bottom to reward diligent folks such as yourself. Any mistakes in this article are mine, not theirs.