usl4j And You
My friend Jeff wrote a thing a while back which contained a cornucopia of truth, one of my favorite bits being the following:
“It’s slow” is the hardest problem you’ll ever debug. “It’s slow” might mean one or more of the number of systems involved in performing a user request is slow. It might mean one or more of the parts of a pipeline of transformations across many machines is slow. “It’s slow” is hard, in part, because the problem statement doesn’t provide many clues to location of the flaw. Partial failures, ones that don’t show up on the graphs you usually look up, are lurking in a dark corner. And, until the degradation becomes very obvious, you won’t receive as many resources (time, money, and tooling) to solve it. Dapper and Zipkin were built for a reason.
I’ve been thinking about this lately, and I think another factor which makes this such a hard problem is that even if you have the ability to segment performance telemetry by space (i.e. which subsystem is slow) it’s not guaranteed that doing so will actually find the problem. As with performance optimization, if you don’t find any hotspots, the problem is often systemic, not local, and as such requires a different set of tools to resolve.
In this post, I’ll introduce you to Little’s Law, the Universal Scalability Law, and usl4j, a Java library for modeling system performance given a small set of real-world measurements.
Little’s Law
First, let’s go over Little’s Law. Little’s Law is a simple equation of the behavior of queues. It formally describes the relationship of queue size (\(N\)), throughput (\(X\)) and latency (\(R\)):
\[\begin{array}{rcl} N & = & XR\\ X & = & N/R\\ R & = & N/X\\ \end{array}\]For example, consider a coffee shop which takes an average of 90 seconds to make an order (\(R=90\)). A customer places an order, on average, every 60 seconds (\(X=1/60\)). The average number of in-flight orders, therefore, is \(N=XR=1/60 \times 90 = 1.5\).
Little’s Law is incredibly helpful in terms of being able to predict systems’ behaviors by modeling them as big-ass queues. A simple auto-scaling system, given a threshold latency of \(R\) seconds, can monitor the number of concurrent requests \(N\) over a set of servers. When the number of requests per second \(X\) begins to approach \(N/R\), the system can bring new servers online to increase the capacity and stay under the threshold latency.
Given any two parameters, Little’s Law allows us to derive the third, but what if we want to predict a system’s behavior given only a single parameter?
The Universal Scalability Law
The Universal Scalability Law, developed by Neil J. Gunther, is a model which combines Amdahl’s Law and Gustafson’s Law to produce a nonlinear model which can be used to predict a system’s behavior:
\[X(N) = \dfrac{\lambda N}{1+\sigma(N-1)+\kappa N(N-1)}\]It describes the expected throughput of a system (\(X\)) at a given level of concurrency (\(N\)) as the nonlinear relationship of three parameters:
- \(\sigma\), the overhead of contention
- \(\kappa\), the overhead of crosstalk
- \(\lambda\), how fast the system operates in ideal conditions
(For a more in-depth explanation, I highly recommend reading Baron Schwartz’s excellent book, Practical Scalability Analysis with the Universal Scalability Law.)
Given a set of USL parameters \(\{\sigma,\kappa,\lambda\}\), we can use the USL equation to pin down one parameter of Little’s Law, allowing us to make predictions given the value of any single parameter:
\[\begin{array}{rcc} R(N) & = & \dfrac{1 + \sigma(N-1) + \kappa N(N-1)}{\lambda}\\ R(X) & = & \dfrac{-\sqrt{X^2 (\kappa^2 + 2 \kappa (\sigma - 2) + \sigma^2) + 2 \lambda X (\kappa - \sigma) + \lambda^2} + \kappa X + \lambda - \sigma X}{2 \kappa X^2}\\ X(R) & = & \dfrac{\sqrt{\sigma^2 + \kappa^2 + 2 \kappa (2 \lambda R + \sigma - 2) - \kappa + \sigma}}{2 \kappa R}\\ N(R) & = & \dfrac{\kappa - \sigma + \sqrt{\sigma^2 + \kappa^2 + 2 \kappa (2 \lambda R + \sigma - 2)}}{2 \kappa}\\ \end{array}\]We can even predict the maximum concurrency of a system:
\[N_{max} = \left\lfloor \sqrt{\dfrac{1 - \sigma}{\kappa}} \right\rfloor\]But where do \(\sigma\), \(\kappa\), and \(\lambda\) come from? In order to determine the USL parameters for a system, we must first gather a set of measurements of the system’s behavior.
Building a model
These measurements must be of two of the three parameters of Little’s Law: mean response time (in seconds), throughput (in requests per second), and concurrency (i.e. the number of concurrent clients).
Because response time tends to be a property of load (i.e. it rises as throughput or concurrency rises), the dependent variable in our tests should be mean response time. This leaves either throughput or concurrency as our independent variable, but thanks to Little’s Law it doesn’t matter which one we use. Because the USL is defined in terms of concurrency (\(N\)) and throughput (\(X\)), it’s more straight-forward to keep these measurements in those terms.
For the purposes of discussion, let’s say we measure throughput as a function of the number of concurrent clients sending requests as fast as they can. After our load testing is done, we should have a set of measurements shaped like this:
| Concurrency | Throughput |
|---|---|
| 1 | 955.16 |
| 2 | 1878.91 |
| 3 | 2688.01 |
| 4 | 3548.68 |
| 5 | 4315.54 |
| 6 | 5130.43 |
| 7 | 5931.37 |
| 8 | 6531.08 |
Next comes the hard part: we need to use a nonlinear solver to generate optimal coefficients for the USL which fit these measurements.
Using usl4j
Luckily for you, I wrote usl4j, a Java library which uses DDogleg’s Levenberg-Marquardt least-squares optimizer to build a fully-parameterized USL model given a set of measurements:
import com.codahale.usl4j.Measurement;
import com.codahale.usl4j.Model;
import java.util.Arrays;
class Example {
void buildModel() {
double[][] points = { {1, 955.16}, {2, 1878.91}, {3, 2688.01} }; // etc.
// Map the points to measurements of concurrency and
// throughput, then build a model from them.
Model model = Arrays.stream(points)
.map(Measurement.ofConcurrency()::andThroughput)
.collect(Model.toModel());
// Predict the throughput for various levels of
// possible concurrency.
for (int i = 10; i < 200; i+=10) {
System.out.printf("At %d concurrent clients, expect %f req/sec\n",
i, model.throughputAtConcurrency(i));
}
}
}
The resulting data looks something like this:
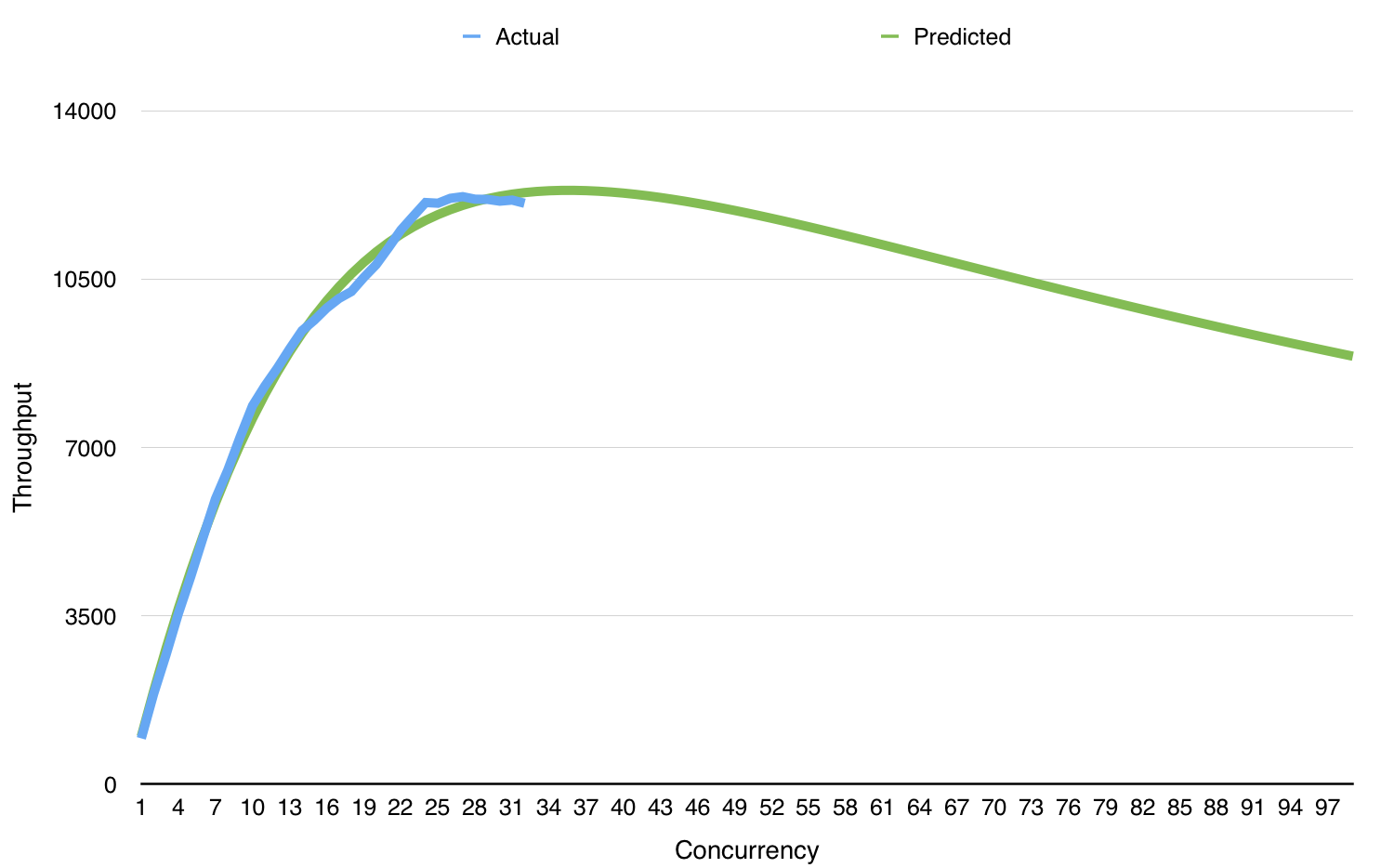
usl4j allows you to calculate all of the parameters of Little’s Law: \(N(X)\), \(N(R)\), \(X(N)\), \(X(R)\), \(R(N)\), \(R(X)\), as well as \(N_\text{max}\) and \(X_\text{max}\).
Continuous Measurement
Because we can build USL models using submaximal testing (i.e. not testing to overload), the measurements we use aren’t necessarily restricted to test bench experiments. We can take real measurements from live systems and continuously build models from them, as building a model from a small set of measurements is very fast (i.e. <100µs).
Building USL models in realtime can augment dashboards and alerting systems with answers to critical questions:
- How close is the system to the predicted maximum throughput or concurrency?
- How close are we to the point at which our latency will be over SLA?
- How much would adding another server help our latency?
Building USL models over historical data allows you to quantitatively answer key questions about how the system has changed over time with regard to scalability:
- A decreased \(\sigma\) value means decreased contention (e.g. better database lock scheduling or a new lock-free data structure).
- A decreased \(\kappa\) value means decreased crosstalk (e.g. removing false cache sharing, or reduced fanout in a distributed system).
- An increased \(\lambda\) value means the system has increased in unloaded performance (e.g. a new compiler optimization or runtime version).
USL For All
Because the USL has a strong physical basis, its parameters can indicate where effort is best spent: increasing \(\sigma\), \(\kappa\), or \(\lambda\). Unlike existing observability tools, the USL can allow you to pinpoint what kind of process is behind “it’s slow”, even if the slowness isn’t limited to a subset of the system.
The USL is a powerful, accessible tool for modeling the behavior of software systems, and it’s my firm hope that making it easily automatable with usl4j leads to its adoption in observability platforms.